Speaker
Description
The investigations of the nanosize magnetic particles and arrays continuously attract academic and technological interest. Their magnetic properties can be varied over a wide range by modifying the nanoparticle shape, size, curvature and separation [1]. While static magnetic properties of a single particle are mostly well understood, their high-frequency spin-wave dynamics still lacks comprehensive theoretical explanation for some important cases [2]. In the given paper the effect of particle curvature on the dipole-exchange oscillations frequency is investigated
We have considered an infinitely long ferromagnetic curvilinear cylinder with elliptical cross-section given by semiaxes a and b, made from ferrite with magnetization $4\pi M$ and biased with external magnetic field H, applied along cylinder semiaxis a. We introduced the modified elliptical coordinate system, according to [3]
\begin{equation}
z = \left(\rho + \frac{{c^2 }}{{4\rho }}\right)\cos \phi , \, y = \left(\rho - \frac{{c^2 }}{{4\rho }}\right)\sin \phi, \, \phi \in [ - \pi ,\pi ], \,
\rho \in \left[\frac{c}{2},\infty \right),c=\sqrt{a^2-b^2}
\end{equation}
In these coordinates the magnetostatic potential inside the ferrite is given by $\Psi _1 (\rho ,\phi ) = \sum\limits_{k = 1}^\infty {\left( {M_k U^k (\rho ,\phi ) + N_k V^k (\rho ,\phi )} \right)} $, where $U(\rho ,\phi ) = \left( {\rho + \frac{{c^2 }}{{4\rho }}} \right)\cos \phi + \frac{1}{{\sqrt { - \mu } }} \left( {\rho - \frac{{c^2 }}{{4\rho }}} \right)\sin \phi $, $V(\rho ,\phi ) = \left( {\rho + \frac{{c^2 }}{{4\rho }}} \right)\cos \phi - \frac{1}{{\sqrt { - \mu } }}\left( {\rho - \frac{{c^2 }}{{4\rho }}} \right)\sin \phi$, and $\mu = \frac{{\omega ^2 - \gamma ^2 H_i (H_i + 4\pi M)}}{{\omega ^2 - \gamma ^2 H_i ^2 }}$ - is the diagonal part of tensor magnetic permeability, $H_{i} = H - 4\pi M \cdot b/(a + b)$, and $\gamma$ is the gyromagnetic ratio.
After applying standard boundary conditions at the lateral surface of the cylinder we get a pair of independent secular equations
\begin{equation}
{(1 - i\sqrt { - \mu } )\left( {a + \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k + (1 + i\sqrt { - \mu } )\left( {a - \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k } = 0,
\end{equation}
\begin{equation}
{ - (i + \sqrt { - \mu } )\left( {a + \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k + (i - \sqrt { - \mu } )\left( {a - \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k } = 0 \,\,(1)
\end{equation}
for the modes with symmetric and antisymmetric spatial distribution with respect to the Z axis.
Eqs. (1) are to be solved for $\mu ^{(nk)}$, and the spin modes eigenfrequencies $\omega ^{(nk)}$ can then be retrieved from the abovementioned expression for $\mu $. Figure 1 demonstrates the effect of cylinder cross-section aspect ratio on the normalized eigenfrequencies. All calculations were made for the YIG biased with external field H=3 kOe. The aspect ratio b/a was taken as a variable parameter. A strong influence of sample’s cross-section curvature (from prolate cylinder to oblate) is clearly visible.
The exchange interaction, which plays crucial role for nanosized particle, was accounted for by the substitution $H_i \to H_i + Dk^2 $, where D is the exchange stiffness and k is the spin-wave transversal wavenumber. The latter was extracted form the peak value of the spatial Fourier transformation of the mode's dynamic magnetization.
Finally, the presented theory was applied to explain the experimental results, published in [4] for the dependence of the spin-mode frequencies on the intensity of the transversal magnetic field measured for the array of nickel nanowires with length L=175 nm and radius R=35 nm by Brillouin light scattering (BLS). The experimental values were found to be in a good accordance with theoretical calculations. Also, our theory convincingly reproduces the characteristic fine structure of the BLS magneto-optical response.
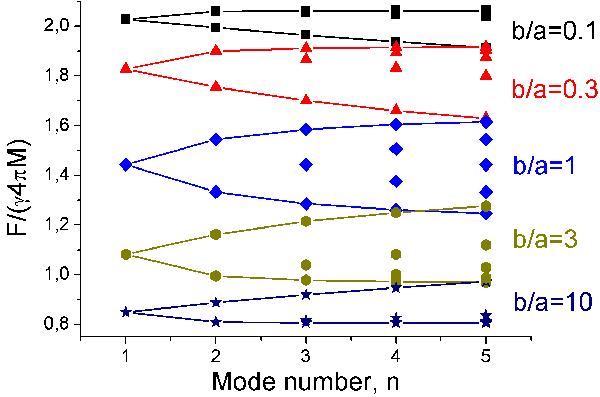
FIG. 1
[1] P. Toneguzzo, G. Viau, F Fiévet, Handbook of Advanced Magnetic Materials, vol.3: Fabrication and Processing, Springer, New York, 2006, p 217-266.
[2] R. Arias, D.L. Mills, Phys. Rev. B, 63 (2001) 134439.
[3] I.V. Zavislyak, G.P. Golovach, M.A. Popov, V.F.Romanyuk, J. Comm. Tech. and Electronics. 51, (2006) 203-211.
[4] A.A. Stashkevich, Y. Roussigne, P. Djemia et al., Phys. Rev. B, 80 (2009) 144406.

