Curvilinear Micromagnetism
Kyiv, Ukraine
Welcome to the international workshop “Curvilinear Micromagnetism” (CurvMag)
The aim of the CurvMag is to join together leading scientists involved in the study of curvature effects in micromagnetism. The scientific program will consist of invited and contributed talks as well as posters, with no parallel sessions.
The workshop is organized under the collaborative research program between Taras Shevchenko National University of Kyiv (Kyiv, Ukraine) and Helmholtz-Zentrum Dresden-Rossendorf e.V. (Dresden, Germany), sponsored by the Alexander von Humboldt foundation (Germany).
Tentative list of invited speakers
- Carvalho-Santos Vagson Luiz (Brazil)
- Dobrovolskiy Oleksandr (Germany)
- Faurie Damien (France)
- Fruchart Olivier (France)
- Hertel Riccardo (France)
- Ivanov Boris (Ukraine)
- Kákay Attila (Germany)
- Kravchuk Volodymyr (Germany)
- Kronast Florian (Germany)
- Landeros Pedro (Chile)
- Lubk Axel (Germany)
- Morozovska Anna (Ukraine)
- Ortix Carmine (Netherlands)
- Pylypovskyi Oleksandr (Ukraine)
- Rodríguez-Quintero Niurka (Spain)
- Saxena Avadh (USA)
- Volkov Oleksii (Germany)

 |
 |
 |
 |
 |
- Alexandra Antoniouk
- Anastasiia Korniienko
- Anna Maria Cucolo
- Anna Morozovska
- Artem Tomilo
- Attila Kákay
- Avadh Saxena
- Axel Lubk
- Bohdan Khromets
- Boris A. Ivanov
- Carmine Ortix
- Damien Faurie
- Denis Sheka
- Denys Kononenko
- Denys Makarov
- Florian Kronast
- Gilbert Santiago Canon Bermudez
- Ivan Kolomiets
- Kostiantyn Yershov
- Maksym Popov
- Niurka Rodríguez-Quintero
- Oksana Busel
- Oleksandr Dobrovolskiy
- Oleksandr Hryshchuk
- Oleksandr Pylypovskyi
- Oleksandr Zaiets
- Oleksii Volkov
- Olexander Belenko
- Olivier Fruchart
- Pedro Landeros
- Petai Pip
- Riccardo Hertel
- Sebastian Castillo
- Stavros Komineas
- Vagson Carvalho-Santos
- Volodymyr Kravchuk
-
-
12:00
→
00:00
Arrival 12h
-
17:00
→
19:00
Registration on-site 2h
-
12:00
→
00:00
-
-
08:30
→
09:00
Registration on-site 30m
-
09:00
→
09:05
Opening of the workshop by Denis Sheka 5m
-
09:05
→
09:10
Welcome words by the President of the Humboldt Club of Ukraine Alexandra Antoniouk 5m
-
09:10
→
09:15
Introductory remarks by Denys Makarov 5m
-
09:15
→
09:45
Topology and transport in nanostructures with curved geometries 30m
Nanostructures are material structures with size in the range of one to a few hundreds of nanometers in at least one spatial dimension. They include zero-dimensional quantum dots, one-dimensional quantum wires and two-dimensional quantum wells. Apart from these conventional material geometries, recent advances in nanostructuring techniques have enabled the synthesis of complex nanoarchitectures: constructs of one- or two-dimensional nanostructures assembled in curved geometries, such as nanotubes and nanohelices.
In this talk, I will first show how the very fundamental quantum mechanical properties of the charge carriers in these nanomaterials are strongly affected by the curved background in which they live. Then I will discuss examples of unique curvature-induced topological and transport properties, including the ballistic anisotropic magnetoresistance effect in non-magnetic and spin-orbit free materials rolled-up into tubes, and the generation of topological insulating phases in corrugated nanowires with Rashba spin-orbit interaction.
Speaker: Dr Carmine Ortix ( Institute for Theoretical Physics, Utrecht University & Physics Department “E. R. Caianiello”, University of Salerno) -
09:45
→
10:15
Effect of Curvature on Topological Defects in Chiral Magnets and Soft Matter 30m
The interplay of geometry and topology underlies many novel and intriguing properties of a variety of soft and hard materials including biological vesicles, nematic liquid crystals and chiral magnets. These materials harbor a gamut of topological defects ranging from domain walls, disclinations, solitons, vortices, skyrmions and merons to monopoles, Dirac strings, hopfions and boojums among many others. I will illustrate this rich interplay with three distinct physical examples. (i) Either the change in the underlying curved manifold or the variation of the Dzyloshinskii-Moriya interaction (DMI) with curvature in magnetic systems. (ii) Controlled motion of liquid crystal skyrmions near curved boundaries using the Q-tensor (as opposed to director) based free energy where the twist acts as the analogue of DMI. (iii) Deformation of biological membranes and vesicles using Canham-Helfrich free energy and Bogomol’nyi decomposition technique to determine equilibrium shapes. Finally, I will briefly describe specific applications of these ideas in spintronics, memory devices as well as drug delivery systems and active matter.
Speaker: Prof. Avadh Saxena (Los Alamos National Lab) -
10:15
→
10:45
Effects of curvature in low-dimensional ferromagnets 30m
Curvilinear geometry of magnetic films and wires enriches physics of their magnetic subsystems with a number of new effects. For example, magnon dispersion relation for a helix-shaped wire demonstrates a linear frequency shift typical for magnets with intrinsic Dzyaloshinskii-Moriya interaction (DMI) [1]; magnetic skyrmion can be stabilized on a spherical shell which is free of any intrinsic DMI [2]; localized curvilinear defect of magnetic film can create a strong pinning potential for a magnetic skyrmion and induce a discrete ladder of energy levels in the pinned skyrmion [3]. These and many other effects can be explained within the general framework [4,5], which introduces a number of curvature induced interactions. The latter are effectively generated by the common energy terms comprising spatial derivatives, e.g. in presence of the curvature the exchange interaction generates the effective DMI and anisotropy, the intrinsic DMI generates effective anisotropy.
Topological magnetic solitons (domain walls, skyrmions, vortices) in curvilinear geometries are of special interest because of the high potential for the spintronics applications. In addition to the curvature induced pinning [3, 6] and driving [7], the topological magnetic solitons in curvilinear systems demonstrate strong effects of chirality symmetry breaking, e.g. coupling of chiralities in spin and physical spaces for a domain wall on a Möbius strip [8], chirality-polarity coupling for a vortex on a spherical shell [9].
An inverse effect of the influence of the magnetic subsystem on the shape of an elastic magnet [10] opens a new area in curvilinear magnetism. The possibility to control the shape and mechanics of the magnet by means of its magnetization creates a promising tool for nanorobotics.[1] D. Sheka et al., PRB 92, 054417 (2015).
[2] V. Kravchuk et al., PRB 94, 144402 (2016).
[3] V. Kravchuk et al., PRL 120, 067201 (2018).
[4] Yu. Gaididei et al., PRL 112, 257203 (2014).
[5] D. Sheka et al., J. Phys. A 48, 125202 (2015).
[6] K. Yershov et al., PRB 92, 104412 (2015).
[7] K. Yershov et al., PRB 98, 060409(R) (2018).
[8] O. Pylypovskyi et al., PRL 114, 197204 (2015).
[9] V. Kravchuk et al., PRB 85, 144433 (2012).
[10] Yu. Gaididei et al., PRB 99, 014404 (2019).Speaker: Dr Volodymyr Kravchuk (Leibniz-Institut für Festkörper- und Werkstoffforschung, IFW Dresden) -
10:45
→
11:10
Coffee-beak 25m
-
11:10
→
11:40
Magnetochiral effects in the dynamics of micromagnetic structures on curved surfaces: finite element modeling 30m
Micromagnetic simulations have reached a high degree of reliability and accuracy over the past years, which allows to ascribe to them predictive power for the magnetic properties of nanostructures. To investigate magnetic processes unfolding as a result of surface curvature, simulations based on finite elements are particularly suited due to their ability to approximate arbitrary geometries. A few years ago, such simulations have revealed extraordinary features regarding the dynamics of vortex-type domain walls in cylindrical soft-magnetic nanotubes with domains oriented along the symmetry axis [1], [2]. The simulations predicted that in these systems the stability and the mobility of field-driven domain walls depend on their chirality, defined by combining the circulation of the vortex in the domain wall with the propagation direction along the tube axis. In particular, domain walls with suitable chirality can attain very high dynamic stability and thereby reach velocities which are significantly larger than the limit that is usually reached by the Walker breakdown [2]. Simulations, supported by analytic studies, also revealed a further type of chiral asymmetry (or non-reciprocity) regarding the propagation of spin waves in magnetic nanotubes with azimuthal magnetization [3], [4].
Both effects, the spin-wave non-reciprocity and the stability of domain walls with specific chirality, are known phenomena in the case of flat thin films of magnetic material with intrinsic Dzyaloshinskii-Moriya interaction (DMI). The observation of these magnetochiral effects in ordinary ferromagnetic materials with curved geometries suggests an analogy between surface curvature and intrinsic DMI [5]. Such a link was also discussed in a number of analytic and numerical studies [6], [7]. In this talk I will review some of these previous findings and present further simulation studies on the dynamics of micromagetic structures on curved surfaces, in ferromagnetic materials with and without intrinsic DMI.
[1] M. Yan, C. Andreas, A. Kákay, F. García-Sánchez, and R. Hertel, “Chiral symmetry breaking and pair-creation mediated Walker breakdown in magnetic nanotubes,” Appl. Phys. Lett. 100, 25, 252401 (2012)
[2] M. Yan, C. Andreas, A. Kákay, F. García-Sánchez, and R. Hertel, “Fast domain wall dynamics in magnetic nanotubes: Suppression of Walker breakdown and Cherenkov-like spin wave emission,” Appl. Phys. Lett. 99, 12, 122505 (2011)
[3] J. A. Otálora, M. Yan, H. Schultheiss, R. Hertel, and A. Kákay, “Curvature-Induced Asymmetric Spin-Wave Dispersion,” Phys. Rev. Lett., 117, 22, 227203 (2016)
[4] J. A. Otálora, M. Yan, H. Schultheiss, R. Hertel, and A. Kákay, “Asymmetric spin-wave dispersion in ferromagnetic nanotubes induced by surface curvature,” Phys. Rev. B, 95, 18, 184415 (2017)
[5] R. Hertel, “Curvature-Induced Magnetochirality,” SPIN, 3, 3, 1340009 (2013)
[6] Y. Gaididei, V. P. Kravchuk, and D. D. Sheka, “Curvature Effects in Thin Magnetic Shells,” Phys. Rev. Lett. 112, 25, 257203 (2014).
[7] V. P. Kravchuk et al., “Topologically stable magnetization states on a spherical shell: Curvature-stabilized skyrmions, Phys. Rev. B. 94, 14, 144402 (2016)Speaker: Dr Riccardo Hertel (Université de Strasbourg, CNRS, IPCMS) -
11:40
→
12:10
Dynamics of magnetic domain wall motion in cylindrical nanowires 30m
The investigation of magnetization dynamics underpinning domain wall motion in one-dimensional conduits, has been a very active research topic over the past two decades. Reports first considered motion under magnetic field, later under spin-polarized current. Experiments have been performed nearly exclusively on thin-film conduits, for ease of fabrication and inspection. This allowed a clear understanding of the physics at play, and went up to demonstrators of a flat race-track memory. In parallel, theory has predicted peculiarities in cylindrical nanowires, with new topologies of domain walls. In particular, one expects that the so-called Bloch-point wall is not subject to Walker-type instabilities, and should allow one to reach the magnonic regime for domain wall motion.
I will present emerging results of magnetization dynamics in such systems. These have been performed based on nanowires made of electroplated soft magnetic materials, with diameter in the range 100-150nm.
Motion under magnetic field may give rise to the dynamic change of topology of domain walls, from Bloch-point type to transverse type, in contradiction with the theoretical predictions. FIG1 illustrates this, featuring a tail-to-tail DW in its thin section. The experiments are partly reproduced by micromagnetic simulations. These results partly put at stake the existing knowledge on such walls.

FIG1. XMCD-PEEM views under zero magnetic field of the shadow of a 140 nm-diameter Fe20Ni80 nanowire. Arrows stand for magnetization in the domains, and the vertical dotted line indicates the diameter modulation. a)-b) and c)-d) are two sequences initialized with a BPW followed by the application of a quasistatic field with strength 12 mT and 24 mT, respectively, as indicated in the final image. e) follows d), after application of -16 mT.Motion under electric current highlights the crucial effect of the OErsted field, an ingredient which had been overlooked in most theoretical works so far. We show that the Oersted field stabilizes Bloch-point domain walls, and selects the sign of their azimuthal circulation. We moved such walls under current, at a speed exceeding 500m/s (See FIG2). Experimental results are reproduced quantitatively using micromagnetic simulations.
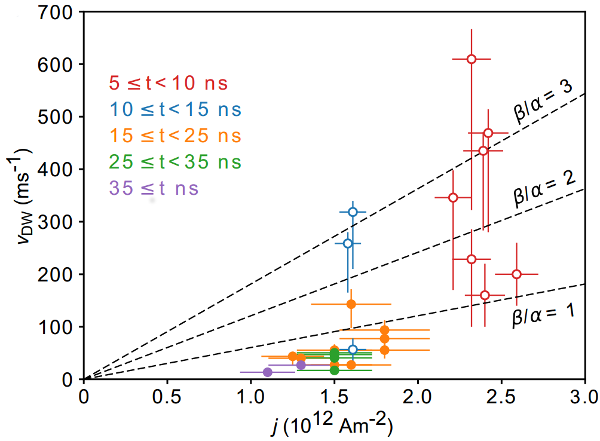
FIG2. Domain wall speed versus density of the electric current flowing in the wire, monitored with either XMCD-PEEM or MFM. Error bars are largely related to the rounded shape of the electric pulses, related to the limited bandwidth of the measurement setupsSpeaker: Dr Olivier Fruchart (Univ. Grenoble Alpes, CNRS, CEA) -
12:10
→
12:40
Magnetism in curved geometries: A challenge for PEEM and other microscopies 30m
At the nanoscale materials exhibit novel properties that are relevant to a wide variety of applications. Geometry can become a design parameter for new electronic, plasmonic or magnetic functionalities. Transforming planar magnetic films to curved objects can introduce magnetochiral properties, similar to the Dzyaloshinskii-Moria interaction. Objects such as hollow cylinders or half spheres can feature faster domain wall motion or the formation of topological spin configurations, such as skyrmions.
Experimental evidence and visualization of curvature induced effects sets a particular challenge for magnetic microscopies such as XPEEM (X-ray photoemission electron microscopy). The relevant length scales are close to resolution limits in the nanometer regime and two- or three-dimensional curved magnetic surfaces add further complexity to magnetic imaging.
This paper will review recent activities using XPEEM to study magnetism in curved geometries. By a combination of element-specific magnetic contrast and high lateral resolution XPEEM offers a unique toolbox for magnetic nanoscale science. Attempts have been made to expand the technique towards the third dimension or magnetic tomography exploiting the magnetic shadow contrast, trying to close a gap in the length scale of magnetic tomographies. An outlook to the near future will show how XPEEM might profit from a new generation of imaging electron detectors with superior dynamic range, highest quantum efficiencies and intrinsic time-resolution. Enabling the technique for studies of magnetization dynamics in curved geometries.
Speaker: Dr Florian Kronast (Helmholtz-Zentrum Berlin) -
12:40
→
14:00
Lunch 1h 20m
-
14:00
→
14:30
Micromagnetic studies of ferromagnetic nanotubes 30m
A review of recent theoretical research in ferromagnetic nanotubes is presented. The focus is on the basic physical behavior that emerges from the micromagnetic theory, from which interesting properties appear [1-6]. Depending on the size parameters, magnetic material, external driving agents, and proper experimental conditions, particular properties are expected, where one can highlight (i) an almost uniform equilibrium state with vortex domains at the tube ends [2], (ii) ultra-fast and chiral domain-wall dynamics [4-5], (iii) ferromagnetic nanorings/nanotubes for magnetic hyperthermia applications [6], where the flux-closure vortex state may be useful to avoid particle agglomeration, while reasonable high values of the specific absorption rate (SAR) are expected. Most of these properties arises from the interplay between the exchange and the magnetostatic energy in the curved ferromagnetic structure. The magnetostatic energy also induces chiral features, which early reported in the motion of a vortex domain wall [4].
[1] P. Landeros, S. Allende, J. Escrig, E. Salcedo, D. Altbir, and E. E. Vogel, Reversal modes in magnetic nanotubes, Appl. Phys. Lett. 90, 102501 (2007).
[2] P. Landeros, O. J. Suarez, A. Cuchillo, and P. Vargas, Equilibrium states and vortex domain wall nucleation in ferromagnetic nanotubes, Phys. Rev. B 79, 024404 (2009).
[3] P. Landeros, P. R. Guzmán, R. Soto-Garrido, and J. Escrig, Magnetostatic fields in tubular nanostructures, J. Phys. D: Appl. Phys. 42, 225002 (2009).
[4] P. Landeros and Á. S. Núñez, Domain wall motion on magnetic nanotubes, J. Appl. Phys. 108, 033917 (2010).
[5] J. A. Otálora, J. A. López-López, P. Vargas, and P. Landeros, Chirality switching and propagation control of a vortex domain wall in ferromagnetic nanotubes, Appl. Phys. Lett. 100, 072407 (2012).
[6] D. F. Gutierrez-Guzman, L. I. Lizardi, J. A. Otálora, and P. Landeros, Hyperthermia in low aspect-ratio magnetic nanotubes for biomedical applications, Appl. Phys. Lett. 110, 133702 (2017).Speaker: Prof. Pedro Landeros (Departamento de Física, Universidad Técnica Federico Santa María) -
14:30
→
15:00
3D reconstruction of magnetic textures in nanomagnets by electron holographic tomography 30m
The fundamental understanding of nanomagnetic phenomena such as domain walls in nanowires requires quantitative magnetization mapping techniques resolving textures down to the nanometer scale in 3D. In our contribution we report on the development of a tomographic reconstruction technique for all Cartesian components of the magnetic induction with a spatial resolution of slightly below 10 nm. To that end we combine off-axis electron holography (EH) and dual tilt-axis tomography in the transmission electron microscope (TEM). Electron holography allows to reconstruct projections of the magnetic flux density by an evaluation of the Aharonov-Bohm phase. The combination with tomography then facilitates the reconstruction of the 3D distribution of the Cartesian component parallel to the respective tilt axis from a tilt series of projections. Employing standard tomographic specimen holders only two perpendicular tilt axis and hence Cartesian components are currently accessible. The third component is evaluated by numerically integrating $\mathrm{div} \vec{B} = 0$. Going one step further, we derive the 3D magnetization distribution and other magnetic quantities such as the magnetization current from the reconstructed 3D magnetic flux density by invoking analytic and numerical micromagnetics.
Using this approach we reconstruct the remnant magnetic configuration of an electro-deposited Co/Cu multilayered nanowire (NW). We particularly reveal several characteristic magnetization states (vortex states or homogeneously magnetized) of the individual Co disk and correlate them to the structural and chemical composition of the NW. We discuss pertaining limits (e.g., resolution) and give an outlook to further instrumental development (such as 3-axis tomography holders). The powerful approach presented here is widely applicable to a broad range of 3D magnetic nanostructures and may help to elucidate a wide range of nanomagnetic configurations.
Speaker: Dr Axel Lubk (IFW Dresden, Germany) -
15:00
→
15:30
Fabrication of 3D nanoarchitectures by focused particle beams 30m
Extending 2D structures into the third dimension has become a general trend in various areas, including photonics, plasmonics and magnetics. This approach provides a means to modify conventional and to launch novel functionalities by tailoring vector potentials inducing anisotropic and chiral effects. Recently, there has been significant progress [1] in the fabrication of free-standing ferromagnetic and superconducting nanostructures by focused particle direct-write techniques, as in part reviewed in [2]. In this respect, 3D shell structures such as framed tubes, spheres, Swiss rolls and helices are especially interesting as they offer unprecedented prospects for nanomagnetism [3] and superconductivity [$4$] because of topology and geometry-controlled effects. Namely, in magnetism, curvilinear geometry brings about two exchange driven interactions - effective anisotropy and antisymmetric vector exchange, i.e. an effective Dzyaloshinskii-Moriya interaction. In addition, another magneto-chiral contribution emerges due to the dipole-dipole interaction. In the case of superconducting nanostructures, the combination of low-dimensionality with a curvilinear geometry allows in principle for the observation of topology-driven effects, such as unconventional phase slips, reversible and irreversible switching, fractional flux-flow instabilities, and the Berezinskii-Kosterlitz-Thouless transition.
In my talk, I will introduce focused ion and electron beam-induced deposition, FIBID and FEBID, respectively, as direct-write techniques suitable for the fabrication of free-standing 3D nanoarchitectures with a resolution in the sub-nm range vertically and 10-20 nm laterally. Next, I will dwell on selected proof-of-concept experiments, technological limitations, and future prospects of using 3D hybrid ferromagnet / superconductor structures with pre-defined shape and curvature in such research areas as microwave engineering [5], superconducting spintronics [6], magnon fluxonics [7], as well as graded-refractive-index spin-wave nano-optics [8].
This work was conducted within the framework of the Actions CM1301 "Chemistry for electron-induced nanofabrication" (CELINA) and CA16218 "Nanoscale coherent hybrid devices for superconducting Quantum technologies" (NANOCOHYBRI) of the European Cooperation in Science and Technology (e-COST).
[1] L. Keller et al., Direct-write of free-form building blocks for artificial magnetic 3D lattices, Sci. Rep. 8 (2018) 6160.
[2] M. Huth, F. Porrati, O. V. Dobrovolskiy, FEBID meets materials science, Microelectron. Engin. 185-186 (2018) 9.
[3] R. Streubel et al., Magnetism in curved geometries, J. Phys. D: Appl. Phys. 49 (2016) 363001.
[4] S. Lösch et al., Microwave radiation detection with an ultra-thin and free standing superconducting niobium nano-helix, ACS Nano (2019).
[5] O. V. Dobrovolskiy et al., Microwave emission from superconducting vortices in Mo/Si superlattices, Nat. Comms. 9, 4927 (2018).
[6] K.-R. Jeon et al., Enhanced spin pumping into superconductors provides evidence for superconducting pure spin currents, Nat. Mater. 17 (2018) 499.
[7] O. V. Dobrovolskiy et al., Magnon-Fluxon interaction in a ferromagnet/superconductor heterostructure, Nat. Phys. (2019).
[8] C. S. Davies et al. Towards graded-index magnonics Phys. Rev. B 92 (2015) 020408.Speaker: Prof. Oleksandr Dobrovolskiy (Physikalisches Institut Goethe University Frankfurt am Main) -
15:30
→
16:00
Curvature effects on the properties of the magnetization in ferromagnetic nanoparticles: from torus to saddle 30m
Nanomagnetism has received a lot of attention in last decades due to the possibility to use nanomagnets in random access memory, data storage, spintronic and magnonic devices, and cancer therapy. These potential applications demand the understanding on the magnetization properties of magnetic nanoparticles, as from experimental as from theoretical point of view. Several works have reported the production and characterization of nanomagnets with different shapes and sizes such as rolled-up magnetic membranes, paraboloidal magnetic caps, spherical and conical nanoparticles, modulated nanomagnets, and cylindrical nanorings, nanodots, nanowires and nanotubes. The production of magnetic nanoparticles with different shapes promotes the description on how geometry influences their magnetic properties in a very important issue. Therefore, the influence of the curvature on the properties of nanosized ferromagnetic systems is a very prominent research area and is under constant investigation. Among main theoretical results in this area, one can cite the appearing of curvature-induced chiral effects, which are responsible for a symmetry breaking of a domain wall motion in magnetic helices, for stabilizing magnetization configurations with topological protection, and for an asymmetry regarding the sign of the wave vector in the dispersion relation of spin-wave propagation in ferromagnetic nanotubes. In addition, curvature afects the domain wall stability and dynamics when it is displacing along curved ferromagnetic nanowires.
In this talk, we will present the contributions that our research group has developed in this area. In particular, we will present the analysis of the non-linear sigma model in curved surfaces. In particular, we will present the influence of curvature in the charcteristic length of solitons in geometries with different curvature properties such as torus, paraboloid and hyperboloid. After, some results describing the magnetic groundstate of ferromagnetic nanotori will be presented. Finally, from the analysis of the remanent magnetization configuration in a ferromagnetic torus with large aspect ratio, we will present our recent results on the description of influence of the curvature on the winding number of vortices when they are stable configurations in geometries with positive and negative curvatures. In this context, we will present the obtention of a vortex-antivortex pair in geometries with variable curvature. Moreover, we will show that geometries with positive curvature can support vortices, while geometries with negative curvature support antivortices as the minimum energy configuration.
Speaker: Dr Vagson Carvalho-Santos (Departamento de Física, Universidade Federal de Viçosa) -
16:00
→
16:30
Coffee-beak 30m
-
16:30
→
16:45
Quantitative MFM on superconducting flux quanta 15m
The quantitative interpretation of MFM data is still a hot topic in the community of scanning probe microscopists. Indeed, the tip magnetic properties are a priori not known and quantitative MFM investigations may only be achieved through phenomenological pictures of the tip-sample interaction, mainly based on the so-called point-probe approximation. In such a model the tip magnetization distribution is sketched as a single magnetic monopole and the measured MFM signal is used to determine the unknown magnetic charge as well as its position within the real tip’s cone.
Here we propose a magnetic characterization of the tip, starting from MFM measurements on superconducting vortices, which appear in type-II superconductors in the mixed state, i.e. in magnetic fields $H_{c1} < H < H_{c2}$ between lower ($H_{c1}(T)$) and upper ($H_{c2}(T)$) critical fields. Each vortex carries out a single flux quantum $\Phi_0=\frac{hc}{2e}$ , where $h$ is the Plank constant, $c$ is the light speed and $e$ is the electron charge. Moreover, while the magnetic field is usually expelled by a superconductor, it can penetrate trough the vortex core and exponential decay by moving out of it, on the scale of the penetration depth $\lambda$. Low temperature MFM is thus the appropriate tool to study the superconducting vortices, being sensitive to the magnetic field decay.
We performed low temperature MFM measurements on 200nm-Nb single layer, driving the simultaneous nucleation of vortices of opposite polarities, namely vortex (V) and antivortex (AV), by profiting of opposite external magnetic field and tip’s field. The measured frequency shift of the oscillating cantilever, due to its interaction with the V-AV pair, will be compared with a phenomenological model built in the framework of the point-probe approximation. By fitting the experimental magnetic profiles, the magnetic tip’s properties (magnetic charge and position) of a commercially available MFM tips (MESP-LM, from Bruker) will be extracted. Finally, as example of quantitative MFM, the results of the fitting procedure will be used to find quantitative information on the out-of-plane magnetization component of Py ferromagnetic thin films. Indeed, such material exhibits a stripe-like configuration of magnetic domains, with magnetization out-of-plane components alternating direction from one stripe to the next.
Speaker: Prof. Anna Maria Cucolo (University of Salerno) -
16:45
→
17:15
Flexomagnetic response of multiferroics 30m
Using direct matrix method we established the structure, including the number of nonzero and independent elements, of the poorly studied flexomagnetic coupling tensor for all 90 magnetic classes. We used the point symmetry of the unit cell, its magnetic symmetry, previously known permutation symmetry, as well as we establish previously unexplored permutation symmetry of the flexomagnetic tensor. For several symmetries, which correspond to the most important for applications multiferroics with nonzero flexomagnetic effect, such as $\mathrm{BiRFeO_3}$ ($\mathrm{R=La, Pr, Eu}$), $\mathrm{Sr_{1-x}Ba_xMnO_3}$, $\mathrm{LiMPO_4}$ ($\mathrm{M = Fe, Co, Ni}$), $\mathrm{TbMn_2O_5}$, $\mathrm{YMnO_3}$, $\mathrm{InMnO_3}$ and $\mathrm{RMn_{1−x}Ga_xO_3}$ ($\mathrm{R=Ho, Y}$), we visualize the effective flexomagnetic response of the bended magnetoelectric plate, analyze its anisotropy and angular dependences. We discuss how the established symmetry can simplify the problem of the flexomagnetic constants determination from experiments, opening the way for its novel applications.
Speaker: Prof. Anna Morozovska (Institute of Physics, National Academy of Sciences of Ukraine) -
17:15
→
18:00
Concluding remarks by Prof Sheka and Dr Makarov / Discussion 45m
-
18:00
→
19:30
Dinner 1h 30m
-
08:30
→
09:00
-
-
08:30
→
09:00
Registration on-site 30m
-
09:00
→
09:30
Curvature induced asymmetric dispersion in nanotubes: handy spin waves in handy tubes 30m
Spin-wave propagation in ferromagnetic nanotubes is fundamentally different than in flat thin films as shown recently [1]. The dispersion relation is asymmetric regarding the sign of the wave vector. As a consequence, spin waves traveling in opposite directions have different wavelength. This purely curvature induced effect originates from the dipole-dipole interaction, namely from the dynamics dipolar volume charges. Such non-reciprocal spin-wave propagation [2] is known for flat thin films with interfacial Dzyalonshiinsky-Moriya interaction or for crystals with a special symmetry (C$_{\text{nv}}$) and bulk Dzyalonshiinsky-Moriya interaction. Here, we will discuss in a nanotube with circular cross section the effect of the individual terms of the divergence on the spin-wave dispersion, through results obtained by finite element micromagnetic simulations. The divergence terms in the cylindrical coordinate system together with the term depending on the mean curvature leads to different asymmetries of the dispersion. We show, that spin waves in nanotubes have chirality or handedness. If the magnetisation in the nanotube is helical, it is also shown that the cylindrical waveguide will also have handedness. This scenario can be compared to that well known from optics: a circular polarised light traveling in a polariser media. We will emphasise the importance of the mean curvature and show that by tailoring it the asymmetry of the dispersion relation can be tuned or even suppressed. It can be concluded that the curvature induced magnetochiral effect with magnetostatic origin can be switched on and off by the manipulation of the surface curvature.
[1] J.A. Otálora, et. al., Phys. Rev. Lett. 117, 227203 (2016).
[2] K. Zakeri, et. al., Phys. Rev. Lett. 104, 137203 (2010).Speaker: Dr Attila Kákay (Helmholtz-Zentrum Dresden - Rossendorf) -
09:30
→
10:00
Arrays of nanostructures on polyimide substrate. Heterogenous strain effect on magnetic properties 30m
Magnetic nanostructures deposited on flexible substrates are of increasing interest for flexible magnetoelectronic applications. In this context, it is crucial to study the links between strain fields and magnetic behavior. In this study, a large area (5 mm × 5 mm) of ferromagnetic nanostructures (nanowires and antidots) have been deposited on top of a polyimide substrate using interference lithography and sputtering processes [1,2].
In order to characterize the strain effect on magnetic properties, we have developed an in situ technique that combines microtensile tests and ferromagnetic resonance. From the shift of resonance spectra as function of applied strain, it is possible to estimate the magneto-mechanical properties. The magnetic resonance frequencies have been measured as function of macroscopic strain applied to the polyimide substrates. We have shown that the resonance shift due to macroscopic strain depends on the kind of system: the effect is stronger for continuous thin film and lower for nanowires. The nanostructuration (nanowires, nano-antidots) induces strain relaxation whose amplitude depend on nanostructures geometrical features [3].
Modelling combining micromagnetism and solid mechanics, describing the strain heterogeneities in such systems, has explained the experimental results. We show that the nanostructuration affects the strain distribution and its mean value in magnetic nanostructures. Therefore, for a given macroscopic strain applied to the substrate, the strain-induced shift of the magnetic resonance field depends on the nanostructures geometry. Especially, the magnetomechanical response depends on the tensile strain direction as referred to the nanostructure orientation.[1] F. Zighem, D. Faurie, M. Belmeguenai, A. Garcia-Sanchez. P. Lupo, A.O. Adeyeye, “Large area periodic ferromagnetic nanowires deposited onto a polymer substrate”, Applied Physics Letters. 111, 052408 (2017)
[2] S. Merabtine, F. Zighem, D. Faurie, A. Garcia-Sanchez, P. Lupo, A.O. Adeyeye, "Multicracking and Magnetic Behavior of Ni80Fe20 Nanowires Deposited onto a Polymer Substrate", Nano letters. 18 (5), 3199-3202 (2018).
[3] N. Challab, F. Zighem, D. Faurie, M. Haboussi, M. Belmeguenai, P. Lupo, A.O. Adeyeye, "Local stiffness effect on ferromagnetic response of nanowires arrays in stretchable systems", Physica Status Solidi – Rapid Research Letters. 13, 1970015 (2019)Speaker: Dr Damien Faurie (LSPM-CNRS, France) -
10:00
→
10:30
Antiferromagnetism for crystals with curved atomic planes: atomic dislocations create spin half-vortices (disclinations) 30m
The standard spin state of antiferromagnets (AFM) contains two magnetic sublattices with equivalent spins $s_1$ and $s_2$, magnetized in the opposite direction such that $s_1+s_2=0$ in the ground state. For their description, so-called Neel vector $l= (s_1-s_2)/|s_1-s_2|$ is used. This kind of ordering is sensitive to crystal lattice dislocations, which destroy the sublattice structure of a perfect antiferromagnet such that $s_1\to s_2$ and $s_2\to s_1$ after a passing around the dislocation along a simple closed counter. Lattice dislocations can be treated as a destruction of the “ideal” geometry and even topology of the atomic planes in a crystal, may give rise to an inhomogeneous spin distribution [1, 2]. Both edge dislocation (atomic plane, broken along some line) and screw dislocation (atomic plane of the form of the Riemann surface for the function $w=z^\nu$ with irrational $\nu$) are the origin of the singular line in the field of the Neel vector $l$. This line is common to the disclinations in the field of vector-director $n$ for nematic liquid crystals: the vector $l$ changes its sing when passing around the AFM disclination line. Spin disclinations were observed in thin films of chromium [3]. For a layered antiferromagnet with a screw dislocation, spin disclination have a macroscopic-sized ferromagnetic core [4].
The review of the static and dynamic properties of the spin non-uniform states caused by different non-ideal topology of the atomic planes of the crystal lattices is done. Single atomic dislocation produces spin disclination, whereas a “compensated” system of dislocations, closed dislocation loop in 3-dimensional (3D) AFM or pair of dislocations loop in 2D AFM produces localized non-uniformity (singular droplet soliton) of the Neel vector. For easy-plane AFM with the form of these solitons is spherical or circular in 3D or 2D cases, accordingly, but it transforms to the ellipsoidal in the presence of in-plane anisotropy. The dynamical solitons with the precession of the Neel vector (e.g., excited by the spin transfer torque) are also possible.[1] I. E. Dzyaloshinsky, JETP Lett. 25, 98 (1977)
[2] A. S. Kovalev and A. M. Kosevich, Sov. J. Low Temp. Phys. 3, 125 (1977)
[3] M. Kleiber, M. Bode, R. Ravlic, and R. Wiesendanger, Phys. Rev. Lett. 85, 4606 (2000)Speaker: Prof. Boris Ivanov (Institute of Magnetism) -
10:30
→
11:00
Coffee-beak 30m
-
11:00
→
11:30
Local and nonlocal interactions in curved ferromagnets 30m
Magnetostatics and engineered anisotropy following the geometry of a magnetic nanoobject result in the coupling of a magnetic texture with geometry and topology of magnetic nanoparticles. It opens a novel ways for developing of novel devices, utilizing the third dimension at nanoscale [1].
In this talk, we discuss the influence of both, local and nonlocal interactions on the state of a ferromagnetic curvilinear shell. In the main order of the shell thickness, magnetostatics can be reduced to a local anisotropy [2]. Depending on the sample geometry, it takes the form of easy-tangential anisotropy in nanowires, biaxial anisotropy in curvilinear ribbons and easy-surface one in infinite shells [3]. We propose a framework allowing to distinguish effects of curvature from spurious effects of curvilinear reference frame. Local curvatures of thin shells put forth additional anisotropy and Dzyaloshinskii-Moria interaction of interfacial symmetry. Magnetostatic energy results in new nonlocal anisotoropic and chiral energy terms in addition to the shape anisotropy in corrugated and curvilinear films. These interactions emerge in shells with nonzero mean curvature. In addition new chiral interaction appears due to the interaction surface and volume magnetostatic charges: it can exist both in flat but rough films and shells. We classify effects of curvature-induced chiral and anisotropic terms in exchange and magnetostatic energies on equilibrium states of magnetization by shell types according to mean and Gauss curvatures.
[1] R. Streubel, P. Fischer, F. Kronast, V. P. Kravchuk, D. D. Sheka, Y. Gaididei, O. G. Schmidt, D. Makarov, J. Phys. D, 49, 363001 (2016)
[2] V. Slastikov, Math. Models Methods Appl. Sci. 15, 1469 (2005); G. Di Fratta, arXiv:1609.08040
[3] Y. Gaididei, A. Goussev, V. P. Kravchuk, O. V. Pylypovskyi, J. M. Robbins, D. Sheka, V. Slastikov, S. Vasylkevych, J. Phys. A. 50, 385401 (2017)Speaker: Dr Oleksandr Pylypovskyi (Taras Shevchenko National University of Kyiv) -
11:30
→
12:00
Experimental observation of exchange-driven chiral effects in parabolic nanostripes 30m
Broken magnetic symmetry is a key aspect in condensed matter physics and in particular in magnetism. It results in the appearance of chiral effects, e.g. topological Hall effect [1] and non-collinear magnetic textures including chiral domain walls and skyrmions [2,3]. These chiral structures are in the heart of novel concepts for magnonics [4], antiferromagnetic spintronics [5], spin-orbitronics [6] and oxitronics [7].
The main origin of the chiral symmetry breaking and thus for the magnetochiral effects in magnetic materials is associated to an antisymmetric exchange interaction, the intrinsic Dzaloshinskii-Moriya interaction (DMI). At present, tailoring of DMI is done rather conventionally by optimizing materials, either doping a bulk single crystal or adjusting interface properties of thin films and multilayers. A viable alternative to the conventional material screening approach can be the exploration of the interplay between geometry and topology. This interplay is of fundamental interest throughout many disciplines in condensed matter physics, including thin layers of superconductors [8] and superfluids [9], nematic liquid crystals [10], cell membranes [11], semiconductors [12]. In the emergent field of curvilinear magnetism chiral effects are associated to the geometrically broken inversion symmetries [13]. Those appear in curvilinear architectures of even conventional materials. There are numerous exciting theoretical predictions of exchange- and magnetostatically-driven curvature effects, which do not rely on any specific modification of the intrinsic magnetic properties, but allow to create non-collinear magnetic textures in a controlled manner by tailoring local curvatures and shapes [14,15]. Until now the predicted chiral effects due to curvatures remained a neat theoretical abstraction.
Here, I review the very first experimental confirmation of the existence of the curvature-induced chiral interaction with exchange origin in a conventional soft ferromagnetic material. It is experimentally explored the theoretical predictions, that the magnetisation reversal of flat parabolic stripes shows a two step process. At the first switching event, a domain wall pinned by the curvature induced exchange-driven DMI is expelled leading to a magnetisation state homogeneous along the parabola's long axis. Measuring the depinning field enables to quantify the effective exchange-driven DMI interaction constant. The magnitude of the effect can be tuned by the parabola's curvature. It is found that the strength of the exchange-induced DMI interaction for the experimentally realised geometries is remarkably strong, namely $\approx 0.4~$mJ/m$^2$, compared the surface induced DMI. The presented study legitimates the predictive power of full-scale micromagnetic simulations to design the properties of ferromagnets through their geometry, thus stabilising chiral textures.
[1] N. Nagaosa, et al., Nature Nanotech. 8, 899 (2013)
[2] U. K. Rößler, et al., Nature 442, 797 (2006)
[3] A. Fert, et al., Nature Rev. Mat. 2, 17031 (2017)
[4] A. V. Chumak, et al., Nature Physics 11, 453 (2015)
[5] T. Jungwirth, et al., Nature Nanotech. 11, 231 (2016)
[6] I. M. Miron, et al., Nature 476, 189 (2011)
[7] V. Garcia, et al., Nature 460, 81 (2009)
[8] J. Tempere, et al., Phys. Rev. B 79, 134516 (2009)
[9] H. Kuratsuji, Phys. Rev. E 85, 031150 (2012)
[10] T. Lopez-Leon, et al., Nature Physics 7, 391 (2011)
[11] H. T. McMahon, et al., Nature 438, 590 (2005)
[12] C. Ortix, Phys. Rev. B 91, 245412 (2015)
[13] Y. Gaididei, et al., Phys. Rev. Lett. 112, 257203 (2014)
[14] J. A. Otálora, et al., Phys. Rev. Lett. 117, 227203 (2016)
[15] V. P. Kravchuk, et al., Phys. Rev. Lett. 120, 067201 (2018)Speaker: Dr Oleksii Volkov (Helmholtz-Zentrum Dresden-Rossendorf) -
12:00
→
12:15
Deposition of homogeneous magnetic layers on 3D non-conductive microstructures 15m
In comparison to planar structures, three-dimensional magnetic micro- and nanostructures offer greater degrees of freedom, showing novel properties such as magneto chirality effects [1], enhanced domain wall dynamics [2] and curvature-induced anisotropy [3]. Exploiting such effects can lead to great benefits for new applications like high-density storage devices, as well as artificial spin systems that provide the possibility of creating and tailoring specific physical properties.
While new insights into realizing the investigation of 3D magnetic systems are highly desired, the fabrication of three-dimensional systems is still challenging due to the lack of reliable methods for the deposition of magnetic thin films on high gradient surfaces.
Here, we present the electroless deposition of NiFe on a 3D-printed, non-conductive microstructure.
Low coercivity and low magnetocrystalline anisotropy are well-known properties of permalloy, making it the ideal material for the study of the influence of three dimensionality on the magnetic properties of a system. In contrast to widely used sputtering, which leads to significant shadowing effects [4], with electroless deposition we can achieve the deposition of homogeneous layers, covering the whole framework (fig.1). This new technique represents an important step towards the experimental realisation of 3D magnetic nanostructures with tailored properties.

FIG. 1[1] Fernández-Pacheco, A., et al., Three-dimensional nanomagnetism. Nature Communications, 2017. 8: p. 15756.
[2] Yan, M., et al., Fast domain wall dynamics in magnetic nanotubes: Suppression of Walker breakdown and Cherenkov-like spin wave emission. Applied Physics Letters, 2011. 99(12): p. 122505.
[3] Streubel, R., et al., Magnetism in curved geometries. Journal of Physics D: Applied Physics, 2016. 49(36): p. 363001.
[4] Donnelly, C., et al., Element-Specific X-Ray Phase Tomography of 3D Structures at the Nanoscale. Physical Review Letters, 2015. 114(11): p. 115501.Speaker: Mr Petai Pip (Empa / Paul Scherrer Institut / ETH Zürich) -
12:15
→
12:30
Propagation of Volume Spin Wave through an Antiferromagnet/Ferromagnet Interface of Finite Thickness 15m
Abridged general form of the boundary conditions at an interface between antiferromagnetic (AFM) and ferromagnetic (FM) materials have been obtained in the continuous medium approximation [1], taking into account the fact that the interface is a composite material with finite thickness $\delta$ which is much less than the length of the spin wave (SW) $\lambda_{\text{sw}}$ and penetration depth $\lambda$ into second material [2]. Three order parameters have been considered inside an interface of finite thickness with magnetizations of both sublattices $\mathbf{M}_{1}$ and $\mathbf{M}_{2}$ of AFM, and magnetization $\mathbf{M}$ of FM. Using these boundary conditions, the excitation of a volume SW has been considered in FM when SW in AFM falls onto this interface. The uniform and non-uniform exchange between all order parameters have been taken into account in the interface energy as the coordinate dependencies of the magnetic parameters characterizing two-sublattice AFM, FM, and the interface region on the coordinate along the axis perpendicular to the interface in the energy. Interconnection between the magnitudes of the amplitudes of the incident spin waves in both sublattices and the reflected spin waves in both sublattices of the two-sublattice AFM have been derived. All possible variants of the energy transfer to the second material in the current system via the Poynting vector have been considered and the dependency between the amplitudes of the incident, transferred and the reflected SWs in the positive cases has been demonstrated [3]. The amplitude coefficients of the scattering and the phases of transmission and reflection of SW through the AFM/FM interface have been derived in general case.
[1] O. P. Busel, O. Yu. Gorobets and Yu. I. Gorobets, “Boundary conditions at the interface of finite thickness between ferromagnetic and antiferromagnetic materials”, J. Magn. Magn. Mater. 462, 226-229 (2018)
[2] V. V. Kruglyak, O. Yu. Gorobets, Yu. I. Gorobets, and A. N. Kuchko, “Magnetization boundary conditions at a ferromagnetic interface of finite thickness”, J. Phys.: Condens. Matter 26, 406001 (2014).
[3] A. I. Akhiezer, V. G. Bar’yakhtar, and S. V. Peletminskii, “Spin waves“ (North-Holland, Amsterdam, 1968).Speaker: Ms Oksana Busel (National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”) -
12:30
→
14:00
Lunch 1h 30m
-
14:00
→
14:15
Shape transformations of elastic ferromagnetic systems 15m
We propose a minimal extension of the anisotropic Heisenberg model in order to describe flexible magnetic systems with coupled magnetic and mechanical subsystems. The interaction between the magnetic and mechanical subsystems is driven by uniaxial anisotropy with the easy-axis oriented along the tangential direction and by the Dzyaloshinskii-Moriya interaction (DMI).
Firstly, we study flexible ferromagnetic wires (rings) [1]. For elastic rings we show that magnetic subsystem can determine the equilibrium shape of the ferromagnet. Depending on the magnetic and elastic parameters and the size of the system one can obtain two different states: the onion state with the quasi-uniform magnetization is typical for small enough rings, while the vortex state with the magnetization oriented tangential to the wire is preferable for large systems.
We also show that the presence of DMI, results in a spontaneous deformation of a flexible magnetic ribbon. The final state is characterizing by the geometrical chirality whose sign is determined by the sign of the DMI constant. Depending on the mechanical, magnetic, and geometric parameters of the system one can obtain two different states: twisted-state with zero curvature of the central line is typical for small DMI constants and narrow ribbons, while the DNA-like state with nonzero curvature of central line is preferable for large DMI constants and wider ribbons. Using in-house developed simulator we build phase diagram of equilibrium states for flexible ribbon.
The theoretical results are verified by means of numerical simulations.
[1] Yu. Gaididei, K. Yershov, D. Sheka, V. Kravchuk, A. Saxena, PRB 99 014404, (2019).
Speaker: Dr Kostiantyn Yershov (Leibniz-Institut für Festkörper- und Werkstoffforschung, IFW Dresden) -
14:15
→
14:30
Dipole-exchange oscillations in transversely magnetized ferromagnetic nanowires of elliptical cross-section 15m
The investigations of the nanosize magnetic particles and arrays continuously attract academic and technological interest. Their magnetic properties can be varied over a wide range by modifying the nanoparticle shape, size, curvature and separation [1]. While static magnetic properties of a single particle are mostly well understood, their high-frequency spin-wave dynamics still lacks comprehensive theoretical explanation for some important cases [2]. In the given paper the effect of particle curvature on the dipole-exchange oscillations frequency is investigated
We have considered an infinitely long ferromagnetic curvilinear cylinder with elliptical cross-section given by semiaxes a and b, made from ferrite with magnetization $4\pi M$ and biased with external magnetic field H, applied along cylinder semiaxis a. We introduced the modified elliptical coordinate system, according to [3]
\begin{equation}
z = \left(\rho + \frac{{c^2 }}{{4\rho }}\right)\cos \phi , \, y = \left(\rho - \frac{{c^2 }}{{4\rho }}\right)\sin \phi, \, \phi \in [ - \pi ,\pi ], \,
\rho \in \left[\frac{c}{2},\infty \right),c=\sqrt{a^2-b^2}
\end{equation}
In these coordinates the magnetostatic potential inside the ferrite is given by $\Psi _1 (\rho ,\phi ) = \sum\limits_{k = 1}^\infty {\left( {M_k U^k (\rho ,\phi ) + N_k V^k (\rho ,\phi )} \right)} $, where $U(\rho ,\phi ) = \left( {\rho + \frac{{c^2 }}{{4\rho }}} \right)\cos \phi + \frac{1}{{\sqrt { - \mu } }} \left( {\rho - \frac{{c^2 }}{{4\rho }}} \right)\sin \phi $, $V(\rho ,\phi ) = \left( {\rho + \frac{{c^2 }}{{4\rho }}} \right)\cos \phi - \frac{1}{{\sqrt { - \mu } }}\left( {\rho - \frac{{c^2 }}{{4\rho }}} \right)\sin \phi$, and $\mu = \frac{{\omega ^2 - \gamma ^2 H_i (H_i + 4\pi M)}}{{\omega ^2 - \gamma ^2 H_i ^2 }}$ - is the diagonal part of tensor magnetic permeability, $H_{i} = H - 4\pi M \cdot b/(a + b)$, and $\gamma$ is the gyromagnetic ratio.
After applying standard boundary conditions at the lateral surface of the cylinder we get a pair of independent secular equations
\begin{equation}
{(1 - i\sqrt { - \mu } )\left( {a + \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k + (1 + i\sqrt { - \mu } )\left( {a - \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k } = 0,
\end{equation}
\begin{equation}
{ - (i + \sqrt { - \mu } )\left( {a + \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k + (i - \sqrt { - \mu } )\left( {a - \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k } = 0 \,\,(1)
\end{equation}
for the modes with symmetric and antisymmetric spatial distribution with respect to the Z axis.
Eqs. (1) are to be solved for $\mu ^{(nk)}$, and the spin modes eigenfrequencies $\omega ^{(nk)}$ can then be retrieved from the abovementioned expression for $\mu $. Figure 1 demonstrates the effect of cylinder cross-section aspect ratio on the normalized eigenfrequencies. All calculations were made for the YIG biased with external field H=3 kOe. The aspect ratio b/a was taken as a variable parameter. A strong influence of sample’s cross-section curvature (from prolate cylinder to oblate) is clearly visible.
The exchange interaction, which plays crucial role for nanosized particle, was accounted for by the substitution $H_i \to H_i + Dk^2 $, where D is the exchange stiffness and k is the spin-wave transversal wavenumber. The latter was extracted form the peak value of the spatial Fourier transformation of the mode's dynamic magnetization.
Finally, the presented theory was applied to explain the experimental results, published in [4] for the dependence of the spin-mode frequencies on the intensity of the transversal magnetic field measured for the array of nickel nanowires with length L=175 nm and radius R=35 nm by Brillouin light scattering (BLS). The experimental values were found to be in a good accordance with theoretical calculations. Also, our theory convincingly reproduces the characteristic fine structure of the BLS magneto-optical response.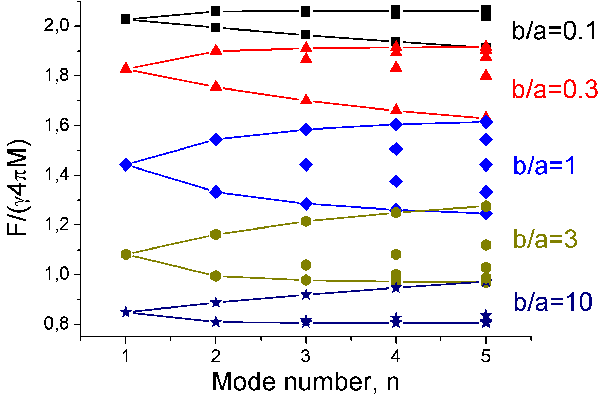
FIG. 1[1] P. Toneguzzo, G. Viau, F Fiévet, Handbook of Advanced Magnetic Materials, vol.3: Fabrication and Processing, Springer, New York, 2006, p 217-266.
[2] R. Arias, D.L. Mills, Phys. Rev. B, 63 (2001) 134439.
[3] I.V. Zavislyak, G.P. Golovach, M.A. Popov, V.F.Romanyuk, J. Comm. Tech. and Electronics. 51, (2006) 203-211.
[4] A.A. Stashkevich, Y. Roussigne, P. Djemia et al., Phys. Rev. B, 80 (2009) 144406.Speaker: Dr Maksym Popov (Faculty of Radio Physics, Electronics and Computer Systems) -
14:30
→
14:45
Role of the shape anisotropy on the magnetization reversal in curved surfaces 15m
In the last years, a strong interest has been focused on the properties of curved magnetic structures. An important aspect of these systems is the possibility of controlling the magnetic behavior at the nanoscale by changing the curvature. This interest has been reinforced by the development of a theory that allows to calculate the exchange energy of nano magnets with arbitrary shapes, which has been used to study the magnetic properties of Möbius stripes, helical wires and DWs in a paraboloidal local bend of nanowires.
In this work, we studied the magnetization reversal process as a function of curvature, in nanotubes with a truncated tubular cross-section. Using a theoretical formalism, we obtain a phase diagram for the DW mechanism as a function of curvature (transversal and vortex-like domain walls). In the ultra thin limit, our results can be interpreted assuming that curvature generates an effective anisotropy in the structure.
Speaker: Dr Sebastián Castillo (Universidad Autónoma de Chile) -
14:45
→
15:00
Band Structure of the Spectrum of the Curvature-Induced One-Dimensional Magnonic Crystal 15m
Magnonic crystals are the artificial periodic structures which can be produced by spatial variations of magnetic parameters such as saturation magnetization, exchange constant or geometrical parameters [1]. They are promising for the control of magnon currents, all-magnon data processing [2] and for logic gates realization [3].
In the current study we consider ferromagnetic wave-shaped nanowire with strong easy-tangential anisotropy and propose new mechanism of magnonic crystal formation due to the periodic curvature. The ground state of magnetization and spin-wave spectrum of this structure can be described using recently developed approach [4] for arbitrary shaped wires. Curvature effects result in two geometry-driven effective interactions: the Dzyaloshinskii-Moriya one and additional anisotropy. These interactions lead to the deviation of magnetization from tangential distribution. Analytically and numerically we calculate the ground state of magnetization in a wide range of curvatures.
The periodic structure of the magnetization ground state plays a role of periodic potential for magnon excitations. The spin-wave band structure is calculated numerically and limit cases of large and small curvatures are solved analytically. With increasing of the curvature, the width of the main gap asymptotically goes to zero by the law $\Delta\Omega_0\propto(\kappa\ell)^{-1}$, with $\kappa$ being the curvature amplitude and $\ell$ being the magnetic length. The widths of the all gaps except the first one decrease with increasing of curvature, the width of the first gap $\Delta\Omega_1$ goes to a constant value $\Delta\Omega_1 \asymp \frac{3}{4}$(in units of frequency of uniform ferromagnetic resonance for straight wire). The latter effect can be of high importance for engineering of magnon waveguides based on the magnetic molecular chains.
[1] S. O. Demokritov and A. N. Slavin (eds.), Magnonics: From Fundamentals to Applications (Topics in Applied Physics), Springer Berlin Heidelberg, Berlin New York (2013)
[2] A. V. Chumak, V. I. Vasyuchka, A. A. Serga, and B. Hillebrands, Nat. Phys., 11, 453 (2015)
[3] T. Schneider, A. A. Serga, B. Leven, B. Hillebrands, R. Stamps, and M. Kostylev, Appl. Phys. Lett.,92, 022505 (2008)
[4] D. D. Sheka, V. P. Kravchuk and Y.Gaididei, J. of Phys. A: Math. and Theor.,48, 125202 (2015)Speaker: Anastasiia Korniienko (Taras Shevchenko National University of Kyiv) -
15:00
→
15:15
Shape influence on statics and linear dynamics of antiferromagnetic textures in curvilinear quasi-one-dimensional spin chains 15m
Modern developments in nanotechnology allow production of artificial curvilinear nanostructures [1] as well as modification of natural nanosized objects with curved geometry [2]. Such objects attract considerable interest for both theoretical and experimental investigation due to their outstanding physical properties. Also, in the last few years interest in antiferromagnets (AFM) has increased due to their advantages over ferromagnets, namely higher characteristic frequencies and absence of macroscopic magnetization.
However, there is still a need for fundamental investigation of AFM curvilinear systems.Our work focuses on the investigation of equilibrium states and linear dynamics of AFM textures in curvilinear AFM one-dimensional spin chains. We show, that the magnetic dipole-dipole interaction results in a hard-tangential anisotropy in a spin chain. In our study we consider two sublattice collinear AFM with slowly varying AFM textures in the frame of generalized sigma-model approach.
We apply the approach [3, 4], recently developed for ferromagnets, to describe equilibrium AFM textures in helix-shaped and ring-shaped spin chains. The binormal distribution of the Neel vector field corresponds to the ground state of an AFM ring-shaped spin chain whereas AFM helix-shaped spin chain has two equilibrium states: (i) quasi-homogeneous and (ii) quasi-binormal. The state (i) appears for helices with curvature less than torsion and state (ii) vice versa. The software package used to determine stability regions of both ground states was SLaSi simulator [5].
We also describe linear excitations of the equilibrium states in helix-shaped and ring-shaped spin chains. We show that magnon spectrum in the AFM ring-shaped spin chain is discrete and each frequency state is four times degenerated. Magnon spectrum of helix-shaped AFM spin chain is characterized by four dispersion branches.[1] R. Streubel, P. Fischer, F. Kronast, V. P. Kravchuk, D. D. Sheka, Y. Gaididei, O. G. Schmidt and D. Makarov, J. Phys. D, 49, 363001, (2016).
[2] K. Mizoguchi, S. Tanaka, M. Ojima, S. Sano, M. Nagatori, H. Sakamoto,
Y. Yonezawa, Y. Aoki, H. Sato, K. Furukawa, T. Nakamura, Journal of the Physical Society of Japan, 76, 043801, (2007).
[3] Y. Gaididei, V. P. Kravchuk, D. D. Sheka, Phys. Rev. Lett., 112, 257203, (2014); D. D. Sheka, V. P. Kravchuk, Y. Gaididei, J. Phys. A, 48, 125202, (2015).
[4] D. D. Sheka, V. P. Kravchuk, K. V. Yershov and Y. Gaididei, Phys. Rev. B, 92, 054417, (2015); O. V. Pylypovskyi, V. P. Kravchuk, D. D. Sheka, D. Makarov, O. G. Schmidt and Y. Gaididei, Phys. Rev. Lett., 114, 197204, (2015); V. P. Kravchuk, U. K. Rößler, O. M. Volkov, D. D. Sheka, J. van den Brink, D. Makarov, H. Fuchs, H. Fangohr and Y. Gaididei, Phys. Rev. B, 94, 144402, (2016).
[5] O. V. Pylypovskyi, D. D. Sheka, V. P. Kravchuk, Y. Gaididei, Journal of Magnetism and Magnetic Materials, 361, 201 – 205, (2014).Speaker: Mr Denys Kononenko (Taras Shevchenko National University of Kyiv) -
15:15
→
15:45
Symmetries shape the currents 30m
Dynamical systems often contain oscillatory forces or depend on periodic potentials. Time or space periodicity is reflected in the properties of these systems through a dependence on the parameters of their periodic terms [1,2]. In this talk it is shown that simple symmetry considerations determine how their properties depend functionally on the amplitudes and the phases of the periodic terms, regardless of whether they are classical or quantum, stochastic or deterministic, dissipative or non-dissipative [3]. It is shown that, by using this formalism, a small set of measurements is enough to obtain the functional form for a wide range of parameters.
[1] J. A. Cuesta, N. R. Quintero, and R. Alvarez-Nodarse, Phys. Rev. X 3, 041014 (2013).
[2] Niurka R. Quintero, J. Cuesta and R. Alvarez-Nodarse, Phys. Rev. E 81, 030102(R) (2010).
[3] J. Casado-Pascual, J. A. Cuesta, N. R. Quintero, and R. Alvarez-Nodarse, Phys. Rev. E 91, 022905 (2015).Speaker: Dr Niurka Rodriguez-Quintero (University of Seville) -
15:45
→
16:15
Coffee-beak 30m
-
16:15
→
17:00
Concluding remarks by Prof Sheka and Dr Makarov / Discussion 45m
-
08:30
→
09:00
-
-
10:00
→
13:00
Departure 3h
-
10:00
→
13:00