Curvilinear Micromagnetism
Kyiv, Ukraine
Welcome to the international workshop “Curvilinear Micromagnetism” (CurvMag)
The aim of the CurvMag is to join together leading scientists involved in the study of curvature effects in micromagnetism. The scientific program will consist of invited and contributed talks as well as posters, with no parallel sessions.
The workshop is organized under the collaborative research program between Taras Shevchenko National University of Kyiv (Kyiv, Ukraine) and Helmholtz-Zentrum Dresden-Rossendorf e.V. (Dresden, Germany), sponsored by the Alexander von Humboldt foundation (Germany).
Tentative list of invited speakers
- Carvalho-Santos Vagson Luiz (Brazil)
- Dobrovolskiy Oleksandr (Germany)
- Faurie Damien (France)
- Fruchart Olivier (France)
- Hertel Riccardo (France)
- Ivanov Boris (Ukraine)
- Kákay Attila (Germany)
- Kravchuk Volodymyr (Germany)
- Kronast Florian (Germany)
- Landeros Pedro (Chile)
- Lubk Axel (Germany)
- Morozovska Anna (Ukraine)
- Ortix Carmine (Netherlands)
- Pylypovskyi Oleksandr (Ukraine)
- Rodríguez-Quintero Niurka (Spain)
- Saxena Avadh (USA)
- Volkov Oleksii (Germany)
 |
 |
 |
 |
 |
- Alexandra Antoniouk
- Anastasiia Korniienko
- Anna Maria Cucolo
- Anna Morozovska
- Artem Tomilo
- Attila Kákay
- Avadh Saxena
- Axel Lubk
- Bohdan Khromets
- Boris A. Ivanov
- Carmine Ortix
- Damien Faurie
- Denis Sheka
- Denys Kononenko
- Denys Makarov
- Florian Kronast
- Gilbert Santiago Canon Bermudez
- Ivan Kolomiets
- Kostiantyn Yershov
- Maksym Popov
- Niurka Rodríguez-Quintero
- Oksana Busel
- Oleksandr Dobrovolskiy
- Oleksandr Hryshchuk
- Oleksandr Pylypovskyi
- Oleksandr Zaiets
- Oleksii Volkov
- Olexander Belenko
- Olivier Fruchart
- Pedro Landeros
- Petai Pip
- Riccardo Hertel
- Sebastian Castillo
- Stavros Komineas
- Vagson Carvalho-Santos
- Volodymyr Kravchuk
-
-
The investigation of magnetization dynamics underpinning domain wall motion in one-dimensional conduits, has been a very active research topic over the past two decades. Reports first considered motion under magnetic field, later under spin-polarized current. Experiments have been performed nearly exclusively on thin-film conduits, for ease of fabrication and inspection. This allowed a clear understanding of the physics at play, and went up to demonstrators of a flat race-track memory. In parallel, theory has predicted peculiarities in cylindrical nanowires, with new topologies of domain walls. In particular, one expects that the so-called Bloch-point wall is not subject to Walker-type instabilities, and should allow one to reach the magnonic regime for domain wall motion.
I will present emerging results of magnetization dynamics in such systems. These have been performed based on nanowires made of electroplated soft magnetic materials, with diameter in the range 100-150nm.
Motion under magnetic field may give rise to the dynamic change of topology of domain walls, from Bloch-point type to transverse type, in contradiction with the theoretical predictions. FIG1 illustrates this, featuring a tail-to-tail DW in its thin section. The experiments are partly reproduced by micromagnetic simulations. These results partly put at stake the existing knowledge on such walls.
FIG1. XMCD-PEEM views under zero magnetic field of the shadow of a 140 nm-diameter Fe20Ni80 nanowire. Arrows stand for magnetization in the domains, and the vertical dotted line indicates the diameter modulation. a)-b) and c)-d) are two sequences initialized with a BPW followed by the application of a quasistatic field with strength 12 mT and 24 mT, respectively, as indicated in the final image. e) follows d), after application of -16 mT.Motion under electric current highlights the crucial effect of the OErsted field, an ingredient which had been overlooked in most theoretical works so far. We show that the Oersted field stabilizes Bloch-point domain walls, and selects the sign of their azimuthal circulation. We moved such walls under current, at a speed exceeding 500m/s (See FIG2). Experimental results are reproduced quantitatively using micromagnetic simulations.
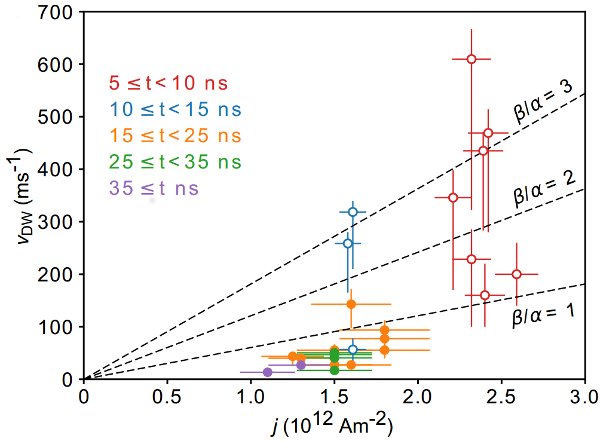
FIG2. Domain wall speed versus density of the electric current flowing in the wire, monitored with either XMCD-PEEM or MFM. Error bars are largely related to the rounded shape of the electric pulses, related to the limited bandwidth of the measurement setupsSpeaker: Dr Olivier Fruchart (Univ. Grenoble Alpes, CNRS, CEA)
-
-
-
In comparison to planar structures, three-dimensional magnetic micro- and nanostructures offer greater degrees of freedom, showing novel properties such as magneto chirality effects [1], enhanced domain wall dynamics [2] and curvature-induced anisotropy [3]. Exploiting such effects can lead to great benefits for new applications like high-density storage devices, as well as artificial spin systems that provide the possibility of creating and tailoring specific physical properties.
While new insights into realizing the investigation of 3D magnetic systems are highly desired, the fabrication of three-dimensional systems is still challenging due to the lack of reliable methods for the deposition of magnetic thin films on high gradient surfaces.
Here, we present the electroless deposition of NiFe on a 3D-printed, non-conductive microstructure.
Low coercivity and low magnetocrystalline anisotropy are well-known properties of permalloy, making it the ideal material for the study of the influence of three dimensionality on the magnetic properties of a system. In contrast to widely used sputtering, which leads to significant shadowing effects [4], with electroless deposition we can achieve the deposition of homogeneous layers, covering the whole framework (fig.1). This new technique represents an important step towards the experimental realisation of 3D magnetic nanostructures with tailored properties.
FIG. 1[1] Fernández-Pacheco, A., et al., Three-dimensional nanomagnetism. Nature Communications, 2017. 8: p. 15756.
[2] Yan, M., et al., Fast domain wall dynamics in magnetic nanotubes: Suppression of Walker breakdown and Cherenkov-like spin wave emission. Applied Physics Letters, 2011. 99(12): p. 122505.
[3] Streubel, R., et al., Magnetism in curved geometries. Journal of Physics D: Applied Physics, 2016. 49(36): p. 363001.
[4] Donnelly, C., et al., Element-Specific X-Ray Phase Tomography of 3D Structures at the Nanoscale. Physical Review Letters, 2015. 114(11): p. 115501.Speaker: Mr Petai Pip (Empa / Paul Scherrer Institut / ETH Zürich) -
The investigations of the nanosize magnetic particles and arrays continuously attract academic and technological interest. Their magnetic properties can be varied over a wide range by modifying the nanoparticle shape, size, curvature and separation [1]. While static magnetic properties of a single particle are mostly well understood, their high-frequency spin-wave dynamics still lacks comprehensive theoretical explanation for some important cases [2]. In the given paper the effect of particle curvature on the dipole-exchange oscillations frequency is investigated
We have considered an infinitely long ferromagnetic curvilinear cylinder with elliptical cross-section given by semiaxes a and b, made from ferrite with magnetization $4\pi M$ and biased with external magnetic field H, applied along cylinder semiaxis a. We introduced the modified elliptical coordinate system, according to [3]
\begin{equation}
z = \left(\rho + \frac{{c^2 }}{{4\rho }}\right)\cos \phi , \, y = \left(\rho - \frac{{c^2 }}{{4\rho }}\right)\sin \phi, \, \phi \in [ - \pi ,\pi ], \,
\rho \in \left[\frac{c}{2},\infty \right),c=\sqrt{a^2-b^2}
\end{equation}
In these coordinates the magnetostatic potential inside the ferrite is given by $\Psi _1 (\rho ,\phi ) = \sum\limits_{k = 1}^\infty {\left( {M_k U^k (\rho ,\phi ) + N_k V^k (\rho ,\phi )} \right)} $, where $U(\rho ,\phi ) = \left( {\rho + \frac{{c^2 }}{{4\rho }}} \right)\cos \phi + \frac{1}{{\sqrt { - \mu } }} \left( {\rho - \frac{{c^2 }}{{4\rho }}} \right)\sin \phi $, $V(\rho ,\phi ) = \left( {\rho + \frac{{c^2 }}{{4\rho }}} \right)\cos \phi - \frac{1}{{\sqrt { - \mu } }}\left( {\rho - \frac{{c^2 }}{{4\rho }}} \right)\sin \phi$, and $\mu = \frac{{\omega ^2 - \gamma ^2 H_i (H_i + 4\pi M)}}{{\omega ^2 - \gamma ^2 H_i ^2 }}$ - is the diagonal part of tensor magnetic permeability, $H_{i} = H - 4\pi M \cdot b/(a + b)$, and $\gamma$ is the gyromagnetic ratio.
After applying standard boundary conditions at the lateral surface of the cylinder we get a pair of independent secular equations
\begin{equation}
{(1 - i\sqrt { - \mu } )\left( {a + \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k + (1 + i\sqrt { - \mu } )\left( {a - \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k } = 0,
\end{equation}
\begin{equation}
{ - (i + \sqrt { - \mu } )\left( {a + \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k + (i - \sqrt { - \mu } )\left( {a - \frac{{ib}}{{\sqrt { - \mu } }}} \right)^k } = 0 \,\,(1)
\end{equation}
for the modes with symmetric and antisymmetric spatial distribution with respect to the Z axis.
Eqs. (1) are to be solved for $\mu ^{(nk)}$, and the spin modes eigenfrequencies $\omega ^{(nk)}$ can then be retrieved from the abovementioned expression for $\mu $. Figure 1 demonstrates the effect of cylinder cross-section aspect ratio on the normalized eigenfrequencies. All calculations were made for the YIG biased with external field H=3 kOe. The aspect ratio b/a was taken as a variable parameter. A strong influence of sample’s cross-section curvature (from prolate cylinder to oblate) is clearly visible.
The exchange interaction, which plays crucial role for nanosized particle, was accounted for by the substitution $H_i \to H_i + Dk^2 $, where D is the exchange stiffness and k is the spin-wave transversal wavenumber. The latter was extracted form the peak value of the spatial Fourier transformation of the mode's dynamic magnetization.
Finally, the presented theory was applied to explain the experimental results, published in [4] for the dependence of the spin-mode frequencies on the intensity of the transversal magnetic field measured for the array of nickel nanowires with length L=175 nm and radius R=35 nm by Brillouin light scattering (BLS). The experimental values were found to be in a good accordance with theoretical calculations. Also, our theory convincingly reproduces the characteristic fine structure of the BLS magneto-optical response.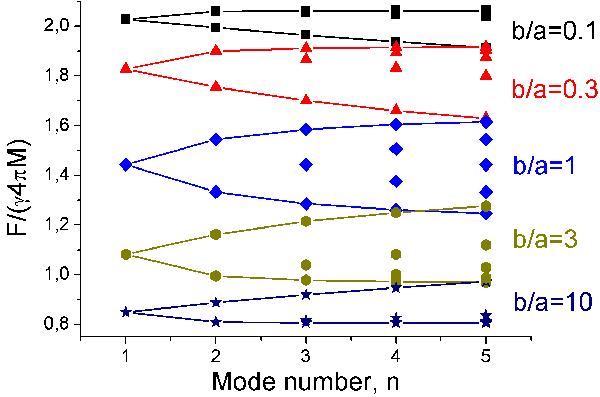
FIG. 1[1] P. Toneguzzo, G. Viau, F Fiévet, Handbook of Advanced Magnetic Materials, vol.3: Fabrication and Processing, Springer, New York, 2006, p 217-266.
[2] R. Arias, D.L. Mills, Phys. Rev. B, 63 (2001) 134439.
[3] I.V. Zavislyak, G.P. Golovach, M.A. Popov, V.F.Romanyuk, J. Comm. Tech. and Electronics. 51, (2006) 203-211.
[4] A.A. Stashkevich, Y. Roussigne, P. Djemia et al., Phys. Rev. B, 80 (2009) 144406.Speaker: Dr Maksym Popov (Faculty of Radio Physics, Electronics and Computer Systems)
-